Dynamic Time Warping with Zig

Read Time: 10 minutes

Reimplementation time! Today I’ll dig into a dynamic time warping implementation using Zig. Its been a language on my radar for awhile now, initially from its usage by TigerBeetle and more recently Ghostty. The new year is as good a time as any to take something new for a spin. So time to get started.

As a refresher, Dynamic Time Warping (DTW) is an algorithm that can be used to compare signals or series. Its main attribute is accounting and adjusting for frequency variance. It has turned into one of my go-to algorithms when trying out a new language. This is a exploratory process, but the goal is to be as idiomatic as possible.

To get started, need to install Zig. The instructions can be found at Getting Started. To note, this post is using Zig 0.14.0.

Like all apps, there is some initial boilerplate. I’ll need the standard library, so I’ll import that as well as setup an alias to the math namespace.

1
2
const std = @import("std");
const math = std.math;

There will be some wrapper code to load data, but starting with the most important piece first, here is the dtw implementation. There is a distance calculation first, simple enough. The prevailing advice appears to be represent 2D arrays as 1D and do the index calculation. For this I made an index() function so I don’t have to worry about screwing up the math in a random spot. Next is the cost function, this is where the real work is done. The primary parameters are two arrays of floats (32bit floats in this case), and a debug flag (for printing the calculation grid if necessary).

The next most important parameter is allocator. If you’ve heard anything about Zig, this is probably one of the more defining characteristics. I won’t cover the entire topic of memory and allocators, but the short version is Zig requires memory allocation/deallocation/management to be handled with allocators. The goal is to make this process explicit, and easier to manage. This provides the power to controlling memory allocation, but helps to limit the types of bugs that can arise in languages that have less control, like C and C++. I honestly spend most of my time in GC’d languages, so this is more management than I typically deal with, but the mechanisms are straight-forward enough to not be burdensome.

A good memory management example are the two lines where I allocate memory for my calculation matrix. var data = try allocator.alloc(f32, matrix_a_len * matrix_b_len); allocates memory, while defer allocator.free(data); ensures the memory is deallocated when the program exits the relevant scope (the function in this case). Zig also support multiple memory allocators with different characteristics, so you can select the best match for your needs. Here, I’d like to make a small call out to std.testing.allocator; an allocator you can use in test code that helps catch memory leaks, truly a life-saver.

After the matrix initialization, I iterate through both sequences, comparing and storing cumulative “best” distances. As an initial pass I’m not interested in implementing some of the typical dtw optimizations. That makes this implementation straight-forward, and a good first step. The below implementation works well for me. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
/// Calculate distance between values
fn distance(a: f32, b: f32) f32 {
  return @abs(a - b);
}

/// Convert a 2D index (a, b) to a 1D position
/// Used when storing a 2D array in a 1D array
fn index(amax: usize, bmax: usize, a: usize, b: usize) usize {
  _ = bmax;
  return (b * amax) + a;
}

/// Calculate cost difference between two sequences (dtw-style)
fn cost(allocator: std.mem.Allocator, stdout: std.fs.File.Writer, debug: bool, a: []const f32, b: []const f32) !f32 {
  // Init matrix
  const matrix_a_len :usize = a.len + 1;
  const matrix_b_len :usize = b.len + 1;

  var data = try allocator.alloc(f32, matrix_a_len * matrix_b_len);
  defer allocator.free(data);

  // Init edges to max value, since they should never be considered in the cost path calculation
  for (1..matrix_a_len) |ai| {
    data[index(matrix_a_len, matrix_b_len, ai, 0)] = math.floatMax(f32);
  }
  for (1..matrix_b_len) |bi| {
    data[index(matrix_a_len, matrix_b_len, 0, bi)] = math.floatMax(f32);
  }

  // Calculate cost matrix
  // NOTE: ai and bi represent index in data (do -1 when referencing into the a and b arrays)
  for (1..matrix_a_len) |ai| {
    for (1..matrix_b_len) |bi| {
      const cell_cost = distance(a[ai - 1], b[bi - 1]);
      data[index(matrix_a_len, matrix_b_len, ai, bi)] =
        cell_cost +
        @min(
          @min(
            data[index(matrix_a_len, matrix_b_len, ai - 1, bi)],
            data[index(matrix_a_len, matrix_b_len, ai, bi - 1)]),
            data[index(matrix_a_len, matrix_b_len, ai - 1, bi - 1)]);
    }
  }

  // Dump cost matrix
  if (debug) {
    try stdout.print("\n", .{});
    for (0..matrix_a_len) |ai| {
      for (0..matrix_b_len) |bi| {
        if (ai == 0 or bi == 0) {
          try stdout.print("  -  ", .{});
        } else {
          try stdout.print("{d:5.1} ", .{ data[index(matrix_a_len, matrix_b_len, ai, bi)] });
        }
      }
      try stdout.print("\n", .{});
    }
  }

  // Return final cost
  return data[a.len * matrix_b_len + b.len];
}

With the primary logic in place, I need some data to go with it. This is the perfect time to learn how to read a file. The goal is to read a text file, and transform the each row into number, then aggregate all rows into a single array. I then return the resulting array to eventually be consumed by the previously defined cost function. This is typically the place where I look for an external csv reader package, but for pedagogical purposes, I’ll just write it myself (not a csv reader, I’ll keep it simple for now).

This comes in two parts. First, readFile will take a file and read the entire file into a single string. Second, this is called by readData. This takes the string, parsing it into rows, then converts each row to a number. These numbers are then used to create a final array of data.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/// Read entire file into a string
fn readFile(allocator: std.mem.Allocator, file_path: []const u8) ![]u8 {
  const file = try std.fs.cwd().openFile(file_path, .{});
  defer file.close();
  const stat = try file.stat();
  return file.readToEndAlloc(allocator, stat.size);
}

/// Count number of times a char appears in a string
fn countChar(s: []const u8, char: u8) usize {
  var count: usize = 0;
  for (s) |c| {
    if (c == char) {
      count += 1;
    }
  }
  return count;
}

/// Read csv file 
fn readData(allocator: std.mem.Allocator, file_name: []const u8) ![]f32 {
  // Read file into string
  const fileContents = try readFile(allocator, file_name);
  defer allocator.free(fileContents);

  // Determine length of data array (lines in file)
  const len = countChar(fileContents, '\n');
  var data = try allocator.alloc(f32, len);

  // Split string into array of floats
  // Where each row contains a single number
  var splitIterator = std.mem.splitScalar(u8, fileContents, '\n');
  var row :usize = 0;
  while(splitIterator.next()) |line| : (row += 1) {
    if (line.len == 0) {
      continue;
    }
    const value = std.fmt.parseFloat(f32, line) catch 0;
    data[row] = value;
  }

  return data;
}

Now, I’m finally to the point where I can put it all together. The app will take two filenames from the command line arguments, load their data and compare. For good measure I include a –debug if I need to view the underlying comparison matrix. Tying back to an earlier section, here is where the memory allocator is defined (GeneralPurposeAllocator in this case). This allocator is then passed to any function that needs to allocate memory.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/// main
pub fn main() !void {
  var gpa = std.heap.GeneralPurposeAllocator(.{}){};
  const allocator = gpa.allocator();
  const stdout = std.io.getStdOut().writer();

  // Get files to load from cliargs
  const args = try std.process.argsAlloc(allocator);
  defer std.process.argsFree(allocator, args);

  if (args.len < 3) {
    try stdout.print("Error: specify two files\n", .{});
    return; 
  }
  const file1 = args[1];
  const file2 = args[2];

  // Determine if in debug mode
  const debug = if (args.len > 3) std.mem.eql(u8, args[3], "--debug") else false;

  // Load files into arrays
  const data1 = try readData(allocator, file1);
  defer allocator.free(data1);
  try stdout.print("data1: {d:1.1}\n", .{data1});

  const data2 = try readData(allocator, file2);
  defer allocator.free(data2);
  try stdout.print("data2: {d:1.1}\n", .{data2});

  // Comparison
  const c = try cost(allocator, stdout, debug, data1, data2);
  try stdout.print("cost: {d}\n", .{c});
}

With the code complete, it is time to test it out. I created some datasets from a modified sin wave. Now I just build and run the app to compare my datasets. I compare each of the five datasets against each other.

1
2
3
4
# build it
$ zig build-exe ./dtw.zig
# run it
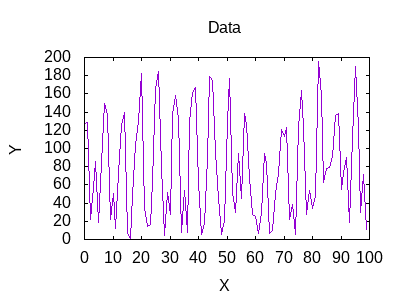
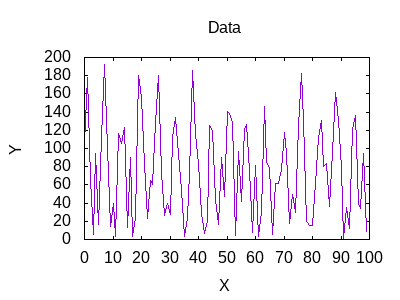
./dtw data1.csv data2.csv

Data 1
Data 2
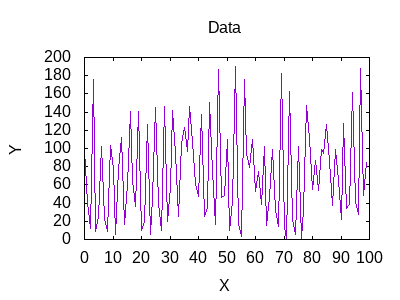
Data 3
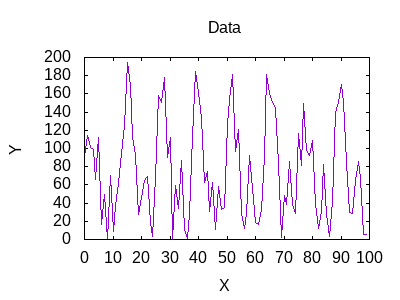
Data 4
Data 5

Here are results of the comparisons.

W1 W2 W3 W4 W5
W1 2234 3385 2802 2879
W2 3170 2853 2896
W3 3548 3825
W4 2457

Using Zig for implementing DTW went smoothly, and was an enjoyable process. I’m pleased with how it all came together. It is still early in the journey, but I enjoy what I’ve seen so far in Zig. Until next time.

Related Posts: